LP Estimated Diffuse Signal Approach to Blind Microphone Geometry Calibration

Methodology

Step-1
Reverberant speech signal is decomposed into the constituent early and late components. $$x_m[n]=x_{m,e}[n]+x_{m,l}[n],~\forall~m$$ Weighted prediction error (WPE) method, which is typically used for speech deverberation is used for the signal decomposition.
Step-2
Late component exhibits diffuse noise properties, which has a distance cue. Spatial cross coherence function of the late part is used to estimate the microphone separation.
Spatial cross coherence function is computed as, $$ \Gamma_{ij}[k]=\frac{\mathbb{E}\{X_{i,l}[k]X_{j,l}^*[k]\}}{\sqrt{\mathbb{E}\{|X_{i,l}[k]|^2\}\mathbb{E}\{|X_{j,l}[k]|^2\} }}$$ where \(X_{i,l}[k]\) is the Fourier transform of \(x_{i,l}[n]\). For a spherically isotropic diffuse noise field, $$ \Gamma_{ij}^s[k]=sinc \left (\frac{2\pi k f_s d_{ij}}{Kc} \right )$$ \(\Gamma_{ij}[k]\) is matched against \(\Gamma_{ij}^s[k]\) for the estimation of distance between microphone pair \(i,j\) $$d_{ij}=\underset{d_{ij}}{\arg\min}~\sum_{k=0}^{K/2} |\Gamma_{ij}[k]-\Gamma_{ij}^s[k]|^2 $$
Step-3
Given estimates of distances between all pairs of microphones, Multi-dimensional scaling (MDS ) is used to estimate the microphone geometry.

Illustration

Signal decomposition

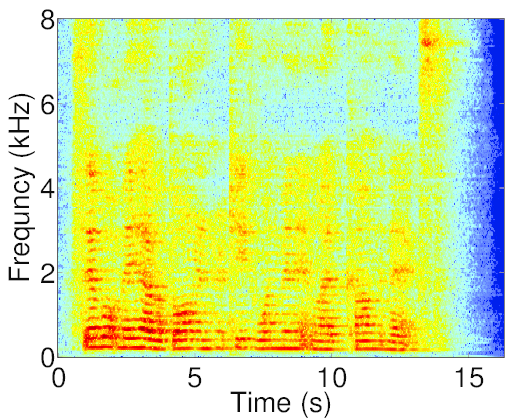
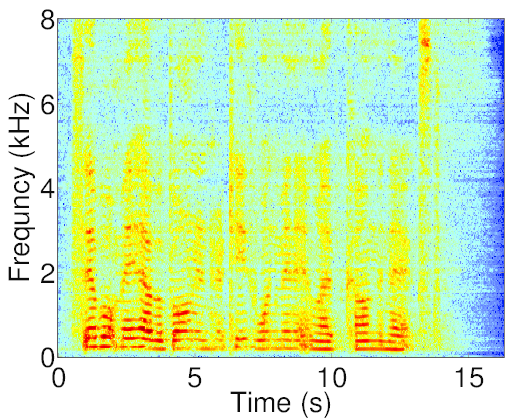
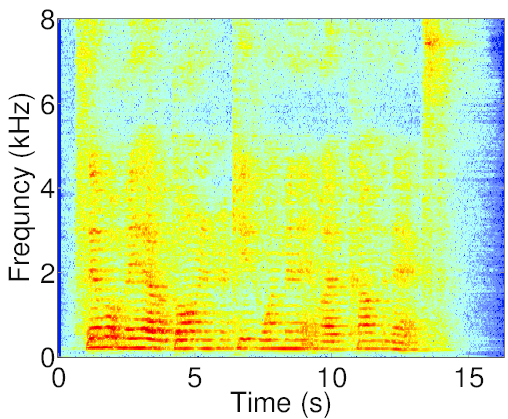
mic signal spectrogram early signal spectrogram late signal spectrogram
Spectrograms of microphone signal, estimated early and late components

Real data experiments

Lab recording example

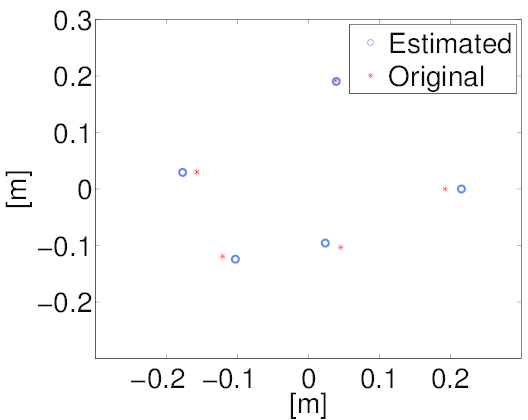
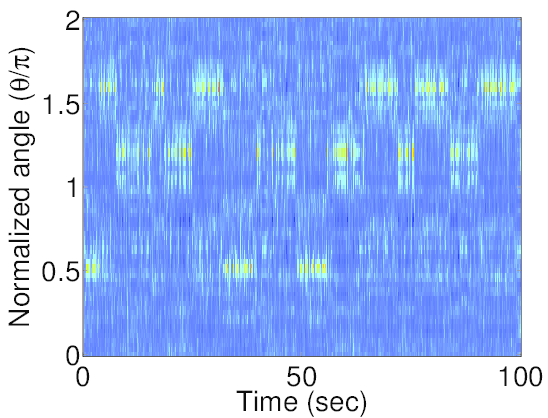
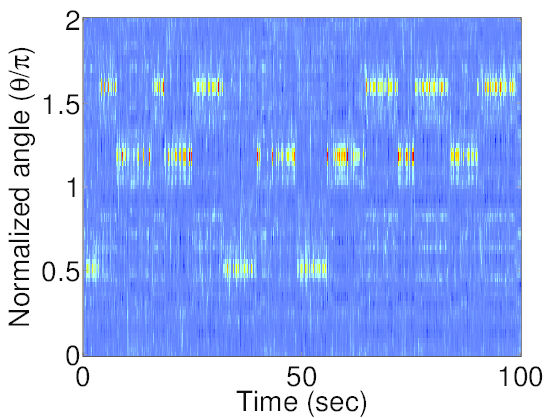
Original and Estimated geometry SRP PHAT response: estimated geometry SRP PHAT response: original geometry

The synthetic meeting recording has a conversation between three participants. Spatial response using estimated microphone geometry is noisy compared to that obtained using the original geometry. However, the locations of peaks are in agreement.

AMI meeting corpus example [link]

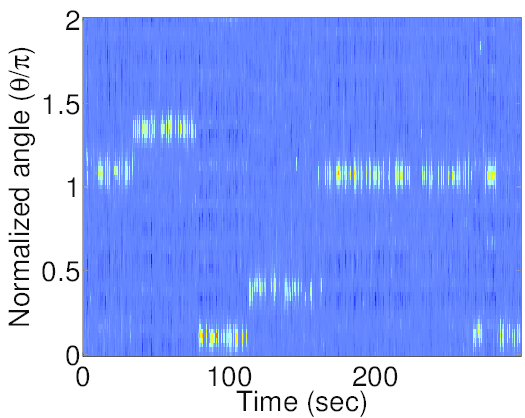
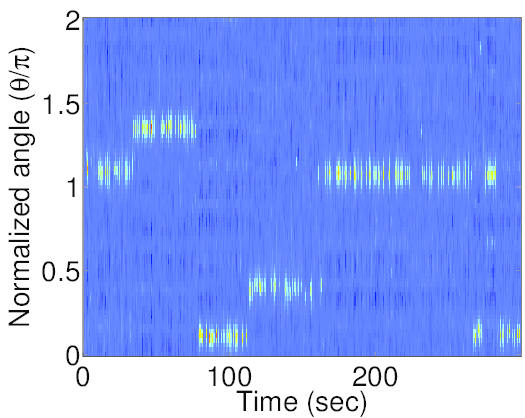
Original and Estimated geometry SRP PHAT response: estimated geometry SRP PHAT response: original geometry

The meeting recording has a conversation between four participants in a conference room at Edinburgh (ES2016a). The response shows the speaker activity as a function of time. Spatial response using estimated microphone geometry closely matches that obtained using the original geometry

Framewise geometry estimation

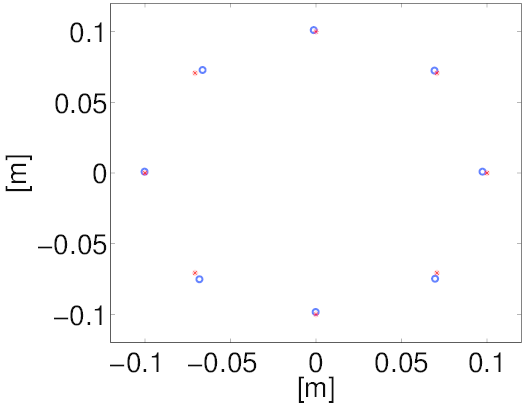
The distance estimates obtained in each frame are used to estimate the geometry of microphones. The geometry estimates from each frame are rotated such that the origin is at the geometric center, first microphone is along the \(x\)-axis and the second microphone is in the positive \(x-y\) plane. Animation below shows the geometry estimates for each frame. (Shown in red is the original microphone geometry)


Implementation

Download Code This is a MATLAB .p file implementation of the geometry estimation algorithm. The syntax for using the file is given below. 


			%%
			% Syntax [M debugInfo]=estimateGeometry(micSignals,samplingRate,speedOfSound,nDim,LPOrder)
			% Inputs:
			%       micSignals: NxM array for signals of M mics, each N sample length
			%       speedOfSound: sound speed in m/s
			%       samplingRate: samplingRate in Hz
			%       nDim: Dimension of the embedding space
			%       LPOrder (optional): 
			%           Default values
			%                   M=8 => L=8
			%                   M=2 => L=32
			%                   others => L=16
			%
			% Outputs:
			%       M: Estimated microphone positions
			%       debugInfo: A structure with fields
			%                  debugInfo.early-early part spectrogram
			%                  debugInfo.late-late part spectrogram
			%                  debugInfo.distanceMatrix-pairwise microphone distance matrix
			%